
Os povos antigos acreditavam que as estrelas eram presas a uma esfera negra que cobria a Terra numa altura desconhecida, mas que poderia ser alcançada, se subíssemos a uma montanha bem alta, ou se atingíssemos os limites da "terra plana". Deste conceito vem a palavra firmamento, usada até hoje, e que dá a idéia de coisa firme, sólida.
Quando o homem conseguiu medir a distância da Terra à Lua, esta esfera foi simplesmente afastada para mais longe, para caber a Lua, mas o conceito básico permaneceu. À medida que foram medidas as distâncias da Terra ao Sol, aos planetas, e posteriormente às estrelas mais próximas, esta esfera foi sendo afastada até que teve de ser abandonada, devido às enormes distâncias envolvidas. Mas sempre existiu a concepção lógica, que se existisse uma esfera, alguma coisa deveria haver do lado de fora. Ainda hoje procuramos por este limite. Apesar de descartada, a idéia da esfera celeste é bastante útil quando analisamos um sistema de coordenadas para a localização das estrelas.
A base do sistema horizontal de coordenadas é o plano definido pela perpendicular à linha de prumo, tangencial à superfície da Terra no ponto O do observador. Imaginemos que este plano se estenda até interceptar a esfera celeste. Definimos então esta interseção como horizonte celeste. Podemos definir também um ponto acima de nossas cabeças, bem no prumo, que chamamos zênite. Por definição o ponto oposto, abaixo de nossos pés é chamado nadir. Neste sistema, adotamos um ponto para início da contagem do ângulo horizontal, o norte, e estabelecemos que a medição dos ângulos se fará no sentido do norte para o leste, sul, oeste até zerar novamente no norte.

O ângulo formado entre o ponto norte e a
interseção do plano que passa pelo zênite, pelo observador O e pela
estrela chamamos azimute. Medimos o ângulo entre o horizonte celeste e a
estrela sobre este plano e obtemos a altura. Assim para cada
estrela teremos um azimute e uma altura. Chamamos a este sistema altazimutal.
Este é um sistema muito usado na astronomia e na navegação
marítma. Só que na navegação, ao contrário da astronomia,
partimos da posição das estrelas para localizar o ponto do
observador sobre a Terra. No sistema equatorial de coordenadas usamos o mesmo sistema de coordenadas geodésicas aplicado para localização de pontos sobre a Terra. Imagine que as linhas de latitude e longitude sejam projetadas desde a Terra até a esfera celeste. Assim teremos um Uma parte do problema está resolvido, mas e a longitude? Quando a Terra gira, o céu vai ficando para trás, e nós perdemos a referência. Na Terra foi estabelecido um ponto para o início da contagem das longitudes: o meridiano
que passa pelo observatório de Greenwich, próximo de Londres,
na Inglaterra.
Na astronomia, o sistema tem uma
deficiência básica: à medida que a Terra gira, tanto o azimute
como a altura variam. Ele pode ser usado na localização de uma
estrela num determinado instante, mas não serve para posicionar
as estrelas num mapa.
O sistema equatorial
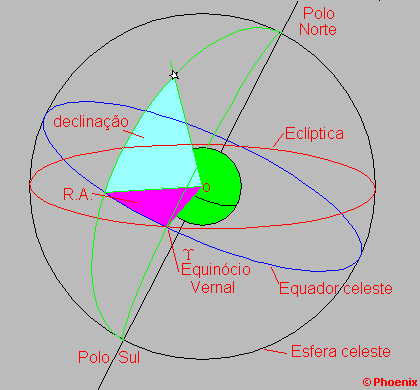
Do mesmo modo, na esfera celeste temos que
estabelecer um ponto fixo para esta marca. Como no céu tudo
está em movimento, escolhemos o ponto onde o Sol, cruzando o
equador celeste, passa do hemisfério sul para o hemisfério
norte, isto é, o ponto
Diferentemente do sistema geodésico, onde a longitude é medida de 0 a 180º E, e de 0 a 180º W, a longitude celeste é medida de 0 a 360º. Mas
quanto tempo leva o céu para, partindo do ponto P, voltar ao mesmo ponto? Um ano sideral! Isto é, um
ano solar mais um dia. Mas o que é o ano sideral? É o tempo de
uma revolução medido, não em relação ao Sol, mas a uma
estrela distante. Vamos estudar o tempo sideral no próximo capítulo.
Já que existe um ano sideral, certamente poderemos ter dia
sideral; claro: basta medir a passagem meridiana de uma estrela!
Resultado: teremos um dia ligeiramente menor que o dia solar,
cerca de 4 minutos. E se dividirmos o dia sideral por 24, teremos
a hora sideral. Mas se o céu se desloca de maneira constante por
todo o ano ele pode ser usado como um relógio, como o relógio
de Sol? Claro! E com vantagem, porque o equador celeste é, por
definição, uma projeção do equador terrestre: ficam no mesmo
plano! Assim podemos medir o tempo com uma precisão de 0,001
segundo!
Para facilitar as coisas, vamos fazer o seguinte: em vez de graduarmos a longitude celeste de 0 a 360º, porque não usamos de 0 a 24 horas? Cada 15º dá exatamente uma hora! Assim estabelecemos no céu uma escala, que mostrará exatamente a hora sideral quando passar pelo meridiano local. Isto significa que podemos acertar nosso relógio sideral, de cada observatório, pelas estrelas. E assim foi feito, até que o advento do rádio permitiu a transmissão de sinais de tempo, com uma precisão ainda maior, para todo o mundo.
Desta maneira todos os mapas celestes foram
graduados, e à longitude celeste, transformada em horas, minutos
e segundos, foi dado o nome de Ascensão Reta,
normalmente abreviado como R.A. já que a maioria dos
bons mapas é importada. A Ascensão Reta é normalmente
representada pela letra grega a e a declinação por d. A
Terra, como um pião girando, tem um ligeiro movimento de
precessão, por isso este sistema não é absolutamente estável, mas
gerando mapas a cada 50 anos, fazemos as pequenas correções
necessárias. Quando tiver um mapa estelar nas mãos, lembre-se
de verificar a data das coordenadas. Você vai encontrar algo
como: Coordenadas para a época 1950.0, ou 2000.0. Isto significa
que as correções foram feitas para o início do ano de 1950 ou
ínicio de 2000. Para determinar as coordenadas do dia com
exatidão, é necessária uma interpolação, somando a
precessão do período.
Todas as cartas celestes adotam este
sistema, aparentemente complicado, mas que simplifica enormemente
a operação de apontar nossos telescópios em busca de corpos
que mal podemos ver. Com telescópio bem orientado e a hora
sideral, podemos encontrar imediatamente planetas e estrelas,
mesmo durante o dia!
Da mesma maneira que usamos o equador celeste como base para o sistema equatorial, podemos usar o plano da eclíptica, o plano da órbita da Terra, projetado na esfera celeste como base de outro sistema: o sistema de coordenadas eclípticas. Neste caso utilizaremos a longitude celeste , designada pela letra grega b , medida
em graus, de 0º a 360º, no sentido leste a partir do equinócio
vernal; e a latitude
celeste , representada por l . Este
sistema é especialmente útil para o estudo das órbitas
planetárias do sistema solar e tem a vantagem de ser muito mais
estável que o sistema equatorial, já que o
"bamboleio" da Terra é eliminado.
Para o estudo da Via Láctea e dos corpos
além de suas fronteiras, um quarto sistema pode ser usado: o
sistema de coordenadas galáticas. Neste caso usaremos o plano da
galáxia para projetar o nosso equador galático na esfera
celeste. A longitude
galática é medida de 0º a 360º no
sentido leste, a partir da direção do centro da galáxia, que
fica na constelação de Sagitarius R.A. = 17h 45m, d = - 28º 56' (2000.0). O Sistema eclíptico
O sistema galático
Podemos determinar também os polos galáticos e desde o equador
galático a latitude
galáxica de maneira similar às
anteriores, isto é, de 0º a +90º para o pólo norte galático,
e de 0º a -90º, para o pólo sul.