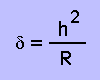O espelho parabolóide
Quando decidimos construir um telescópio mais curto, isto é, com uma relação focal (f/D) menor que o valor limite calculado, nos deparamos com os problemas da aberração esférica  . A construção de um telescópio mais curto pode ser imposta por limitações de tamanho do tubo, incluindo aí a construção de um arranjo Cassegrain, ou simplesmente a obtenção de um aparelho mais luminoso, para a observação de cometas, galáxias e nebulosas. Desde que ele não seja muito curto, o polimento de um espelho parabolóide não apresenta grande dificuldade.
. A construção de um telescópio mais curto pode ser imposta por limitações de tamanho do tubo, incluindo aí a construção de um arranjo Cassegrain, ou simplesmente a obtenção de um aparelho mais luminoso, para a observação de cometas, galáxias e nebulosas. Desde que ele não seja muito curto, o polimento de um espelho parabolóide não apresenta grande dificuldade.
A aberração esférica forma em torno do ponto focal de um espelho uma imagem deformada de um objeto suposto no infinito, não num plano, mas numa superfície cáustica  , como uma corneta. Esta superfície é gerada pela rotação, em torno do eixo óptico, da curva que contém os focos de cada raio luminoso à medida que o diâmetro da objetiva aumenta. Esta aberração cria uma imagem completamente distorcida do objeto, impossível de ser visualizada.
, como uma corneta. Esta superfície é gerada pela rotação, em torno do eixo óptico, da curva que contém os focos de cada raio luminoso à medida que o diâmetro da objetiva aumenta. Esta aberração cria uma imagem completamente distorcida do objeto, impossível de ser visualizada.
Para corrigir este problema, seremos obrigados a deformar a objetiva, de modo a compensar o deslocamento dos focos individuais e juntá-los no ponto focal. A curva matemática que atende a este requisito é a parábola. Assim nossa objetiva será uma superfície parabolóide, ou melhor, um parabolóide de revolução. A maioria dos livros faz referência a uma superfície parabólica, o que a rigor não existe. A parábola é uma curva plana! Do mesmo modo não deveríamos dizer "antena parabólica" e sim "antena parabolóide", já que ela tem três dimensões.
A diferença entre um espelho parabolóide e um esférico é mínima: cerca de 0,4 milésimos de milímetro (0,4m) mais abaixado nas bordas para um espelho de 180 mm f/D=6. Se medido pelo raio médio de curvatura  , a diferença se reduz a 1/4 deste valor.
, a diferença se reduz a 1/4 deste valor.
Se dois espelhos destas dimensões, um esférico e um parabolóide, forem colocados lado a lado, é praticamente impossível por meio de instrumentos mecânicos (paquímetros, micrômetros ou esferômetros) identificar cada um. Somente um instrumento óptico poderá medir a diferença.
A parabolização de um espelho não consegue alterar a sua relação focal.
Segundo Jean Texereau, a partir de um espelho esférico poderemos fazer a parabolização de três maneiras distintas:
1- O método clássico consiste em fazer movimentos  específicos do espelho sobre o "pitch-lap". Se necessário afundar o centro, concentre mais cursos sobre as bordas da ferramenta. Para abaixar a borda, concentre os cursos no centro da ferramenta. A cada dez minutos de trabalho, pare e teste o espelho.
específicos do espelho sobre o "pitch-lap". Se necessário afundar o centro, concentre mais cursos sobre as bordas da ferramenta. Para abaixar a borda, concentre os cursos no centro da ferramenta. A cada dez minutos de trabalho, pare e teste o espelho.
2- Uma alternativa, especialmente útil para espelhos de grande diâmetro, é usar uma ferramenta menor sobre o espelho. Faça um "pitch-lap" com metade do diâmetro do espelho e trabalhe sobre as regiões indicadas  . Este método tem a desvantagem de aumentar as micro-ondulações na superfície e é mais demorado, mas torna o trabalho mais leve. Teste o espelho a cada 15 minutos de polimento.
. Este método tem a desvantagem de aumentar as micro-ondulações na superfície e é mais demorado, mas torna o trabalho mais leve. Teste o espelho a cada 15 minutos de polimento.
3- O método de compressões é usado tanto na parabolização como nas correções de parábolas defeituosas. Consiste em usar o "pitch-lap" sobre o espelho, exercendo a pressão das mãos para obter o efeito desejado. Para afundar o centro  pressione a mão que está sobre o centro do espelho. Os cursos devem se limitar a 1/3 do diâmetro. Para rebater a borda
pressione a mão que está sobre o centro do espelho. Os cursos devem se limitar a 1/3 do diâmetro. Para rebater a borda  trabalhe sobre a borda do espelho usando pressões iguais das mãos. A cada dez minutos, pare o polimento e faça o teste do espelho.
trabalhe sobre a borda do espelho usando pressões iguais das mãos. A cada dez minutos, pare o polimento e faça o teste do espelho.
Mas como poderemos medir e avaliar as deformações do espelho? Vamos medir a deformação da superfície focal e comparar com os valores teóricos calculados para a nossa objetiva.
Nos espelhos de telescópios aquela superfície cáustica tem uma pequena "profundidade" d, que pode ser calculada pela fórmula:
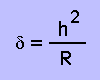
Onde h é a distância do centro e R o raio de curvatura da superfície do espelho (o dobro da distância focal).
Se um espelho esférico cria esta aberração para um objeto no infinito, o inverso também é verdadeiro: um espelho parabolóide irá criar a mesma aberração para um objeto colocado no centro de curvatura, só que invertida. Nós vamos usar esta característica para medir nosso espelho. Usaremos uma escala graduada em milímetros fixada ao lado do parafuso de deslocamento da mesa do aparelho de Foucault para medir cada zona de incidência da luz e corrigir a curvatura se necessário. Como o passo do parafuso é de um milímetro e o disco graduado foi dividido em 10 setores, poderemos obter leituras de 0,1 mm.
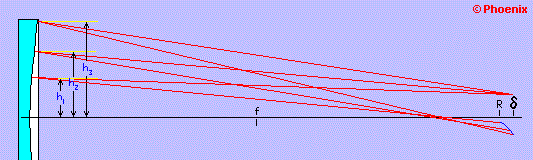
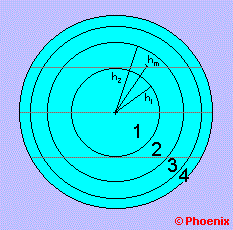
Como seria muito difícil uma medida para cada valor de h, o teste do espelho será feito por zonas, e usaremos o valor médio de cada zona hm para os cálculos. O número de zonas não deve ser muito grande, senão a largura de cada zona ficaria muito estreita, o que poderia prejudicar sua visibilidade. À medida que nos afastamos do centro do espelho a zona medida tem uma área maior, e assim uma maior influência sobre a imagem. Para aumentar a precisão da medida faremos então zonas progressivamente mais estreitas, mantendo um limite mínimo de 15 mm para a borda. Para testar um espelho de 180 mm - f/D=6, poderíamos adotar, por exemplo, 4 zonas de 30, 55, 75 e 90 mm de raio a partir do centro. O raio de curvatura seria R = 2 x 6 x 180 = 2.160 mm.
Para calcular os valores de d, basta encontrar o valor médio hm para cada zona, o valor de R e aplicar na fórmula. Feito isso teremos:
| Zona | h | hm | d |
| 1 | 30 | 15,0 | 0,1 |
| 2 | 55 | 42,5 | 0,8 |
| 3 | 75 | 65,0 | 2,0 |
| 4 | 90 | 82,5 | 3,2 |
Como podemos ver, a diferença entre os pontos focais é de apenas 3,1 mm. Baseado nestes dados podemos agora construir uma máscara com janelas definindo cada zona. Alguns amadores preferem usar apenas uma régua com indicadores das zonas, mas o sistema de janelas é mais preciso.
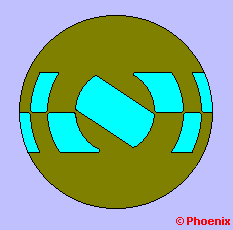
Esta máscara será colocada sobre o espelho durante o teste. No caso do espelho esférico, vimos que toda a superfície era escurecida simultaneamente quando a faca era posicionada sobre o foco. No espelho parabolóide temos um "foco" distinto para cada zona. Vamos procurar então o ponto onde as janelas simétricas tenham a mesma tonalidade e fazer a leitura. Use uma seqüência coerente e faça anotações das medidas obtidas.
Como o posicionamento do aparelho de Foucault pode variar a cada teste, usaremos sempre o valor relativo das medições. Para isso basta definir uma das zonas como padrão, encontrar o valor da diferença para o valor desejado e somar ou subtrair da diferença. Deste modo encontraremos os valores para cada zona. Uma folha de teste deve ser numerada, datada e preenchida para cada ensaio, de modo a permitir o acompanhamento do trabalho e sua evolução.
Para facilitar este procedimento você pode baixar e usar a planilha  disponível no nosso site.
disponível no nosso site.
A folha de controle
A folha de controle deve ter um quadro para as anotações dos dados básicos, dos valores medidos e das correções feitas. Estes dados nos permitirão avaliar o perfil do espelho e programar as correções.
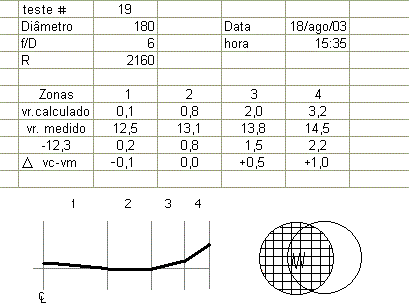
Na folha de controle anotamos os valores calculados e os valores relativos medidos. Escolhemos arbitrariamente a Zona 2 para referência e encontramos o valor da diferença vr.medido - vr.calculado de 12,3. Poderíamos ter escolhido qualquer outra zona para esta referência, mas escolha uma que distribua melhor os erros. Subtraindo este valor de todas as medições vamos encontrar o valor absoluto para cada zona. Na linha seguinte calculamos as diferenças D, subtraímos o valor medido e encontramos as distorções. Estes valores nos permitem traçar um semiperfil do espelho. Quando o valor é negativo significa que a distância focal está maior que a desejada, assim traçamos uma linha descendente na zona 1. Na zona 2 o valor é o de referência, logo nosso perfil será plano. O valor positivo para a zona 3 nos indica uma distância focal menor que a buscada, traçamos uma linha ligeiramente ascendente. Finalmente o valor da zona 4 é positivo e relativamente grande, traçamos uma linha ascendente com uma inclinação proporcionalmente maior. Este perfil não obedece rigorosamente as dimensões, mas nos dá uma excelente idéia da forma atual do nosso espelho: uma borda alta! e nos ajuda a planejar as próximas ações corretivas.
Anote o que deve ser feito e escolha o tipo de movimento  mais adequado para correção de uma borda alta. Trabalhe de 5 a 10 minutos e faça novo teste.
mais adequado para correção de uma borda alta. Trabalhe de 5 a 10 minutos e faça novo teste.
Estas anotações serão importantes para avaliar o resultado de cada ação. É comum tentarmos uma correção e agravar o problema. A experiência adquirida é que nos vai permitir evoluir para a forma desejada.
Nosso objetivo será o de obter um erro máximo na faixa de cinco centésimos de milímetro antes de fazer a análise final.
 . A construção de um telescópio mais curto pode ser imposta por limitações de tamanho do tubo, incluindo aí a construção de um arranjo Cassegrain, ou simplesmente a obtenção de um aparelho mais luminoso, para a observação de cometas, galáxias e nebulosas. Desde que ele não seja muito curto, o polimento de um espelho parabolóide não apresenta grande dificuldade.
. A construção de um telescópio mais curto pode ser imposta por limitações de tamanho do tubo, incluindo aí a construção de um arranjo Cassegrain, ou simplesmente a obtenção de um aparelho mais luminoso, para a observação de cometas, galáxias e nebulosas. Desde que ele não seja muito curto, o polimento de um espelho parabolóide não apresenta grande dificuldade.