Onde estou?
Dúvidas
e Perguntas?
Objetivo
Determinar nossa localização sobre a
Terra (Latitude e Longitude).
Considerações
"Onde estou?", pode parecer uma pergunta insensata, porque
naturalmente todos sabemos onde estamos em um determinado momento, mas como
poderemos informar a alguém qual é este lugar? Uma maneira usual é informar
nosso endereço. Se soubermos o país, o estado, a cidade, o bairro, a rua e o
número da casa, poderemos ser encontrados em qualquer lugar do mundo. Mas e
se não estivermos numa cidade, e sim em uma fazenda, na selva ou no mar? A
única maneira será informar nossas coordenadas sobre a Terra.
Você já deve ter observado que os mapas são graduados em
latitudes, de 0 a 90 graus para o norte ou para o sul, a partir do
equador, e em longitudes, de 0 a 180 graus a leste ou a oeste do
meridiano que passa por Greenwich, na Inglaterra. Meridiano é a linha
imaginária que vai de um pólo ao outro. Este meridiano foi definido como
meridiano zero. A determinação das coordenadas de um ponto é feita,
medindo-se os ângulos entre este ponto e o equador (latitude) e do ponto ao
meridiano de origem (longitude). Este sistema de coordenadas é chamado de Sistema
de Coordenadas Geográficas.
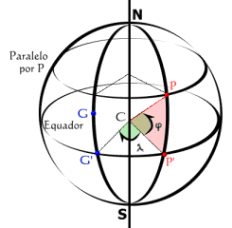 |
Coordenadas
geográficas da Terra.
Na figura
ilustramos: ponto G no meridiano-de-origem (Greenwich) e
ponto P genérico (fora dos pólos) tendo latitude j
e
longitude
l.
Os arcos medem ângulos:
Arco P'P = j,
latitude de P (de 0 a 90º, positiva ao Norte, negativa ao Sul).
Arco G'P' = l,
longitude geográfica de P (de 0 a 180º, positiva a W de Greenwich,
negativa a E).
Na figura é l
= ângulo G'CP'. |
Esse sistema cobre toda a Terra e tem a vantagem de
especificar cada ponto da superfície por duas coordenadas que não se repetem
em outro local, evitando erros de endereçamento. Além disso o sistema de
coordenadas permite que, a partir de uma listagem de dados, se construa um
mapa.
Histórico
Os gregos e os romanos faziam seus mapas medindo as distâncias entre os
pontos e colocando marcos para orientação. A milha romana, uma medida de
distância muito usada, equivalente a 1 440 metros, tem esta origem: uma
centúria (grupo de cem soldados) marchava 1 000 passos e aí era instalado um
marco numerado. Alguns deles existem até hoje na Via Appia, em Roma, na
Itália.
O primeiro cálculo do tamanho da Terra foi feito depois que Erastóstenes de
Cirene (~220 anos A.C.) mandou medir a distância entre Siene e um lugar na
Alexandria, 804 quilômetros ao norte.
Quase todo o antigo Império Romano foi demarcado assim.
Mas com o desenvolvimento das navegações, as distâncias
percorridas aumentaram muito e a medição no mar era impossível. Neste ponto
o conhecimento astronômico se tornou imprescindível. Astrônomos,
matemáticos e cartógrafos foram contratados pelos reis e definiram os
procedimentos de medição. Os portugueses e espanhóis foram precursores das
navegações baseados em "localização por estrelas" e
principalmente pela posição do Sol, e levavam sempre um astrônomo para
fazer este trabalho. Isto é feito pelos marinheiros até hoje, usando um sextante.
Este procedimento nos permite encontrar a latitude de um lugar.
Mas o mesmo procedimento não pode ser usado para encontrar a longitude! A Terra gira no espaço e não existe um referencial fixo!
Por isso as navegações eram feitas com grande imprecisão no sentido da
longitude. Elas eram estimadas em função do tempo e da velocidade do navio.
O tempo era medido com ampulhetas e a distância com uma corda fina, lançada
na água, onde nós marcavam as divisões. Até hoje a velocidade dos barcos e
aviões são registradas em nós (milhas marítimas por hora). Talvez por isso
o Brasil tenha sido descoberto! A única maneira de descobrir a diferença
angular entre dois meridianos seria medir a hora local e comparar com a hora
do meridiano zero. Como não existia um cronômetro naquela época, era
impossível saber a hora de Greenwich. Determinar a hora local é fácil:
quando o Sol está mais alto no céu é o meio-dia local. Este ponto mais alto
ocorre sempre sobre o meridiano que passa pela vertical do lugar. Por isso
este momento é chamado de passagem meridiana do Sol. Usando tabelas de
ocultação de estrelas pela Lua e as ocultações dos satélites de Júpiter,
os astrônomos do século XVI conseguiram determinar as coordenadas de vários
pontos da Terra. Mas a invenção do relógio com escapamento de âncora foi
que determinou o procedimento definitivo para este trabalho. A invenção do
rádio veio complementar este recurso e algumas estações transmitem sinais
de tempo padrão para todo o mundo.
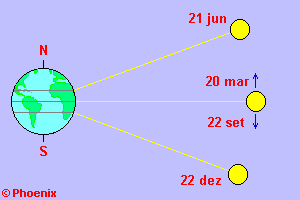
Baseados na posição do Sol nós poderemos encontrar estes
dados com uma precisão razoável. Se o procedimento for feito nos dias de
equinócios (20-mar/22-set) ou de solstícios (21-jun/22-dez) as posições do
Sol são conhecidas e facilitarão a tarefa. Para os outros dias do ano será
necessária uma tabela de posições do Sol, como a publicada no Anuário de
Astronomia do Observatório Nacional, ou calculada por programas de computador. Se precisar mande-nos um e-mail.
Para executar os procedimentos, peça a ajuda e supervisão de um professor que tenha uma calculadora científica que tenha a função arco tangente para encontrar os ângulos e fazer as conversões de tempo e de ângulos.
Material
-
cadeira
- grampo de carpinteiro
- trena com escala em milímetros
- prumo de ponta (pode ser usada uma chumbada piramidal)
- pregos.
- calculadora científica
- relógio com ponteiro de segundos
- anteparo (tampa de lata de 10 cm de diâmetro com furo de 3 mm)
- mapas para ilustrar as coordenadas e obter a posição estimada.
Preparação
Usando um prego grosso, faça um furo
no centro da tampa de lata e dobre um pedaço da lateral de modo que depois de
fixada com o grampo ao espaldar da cadeira, ela fique mais ou menos
perpendicular ao Sol do meio dia.
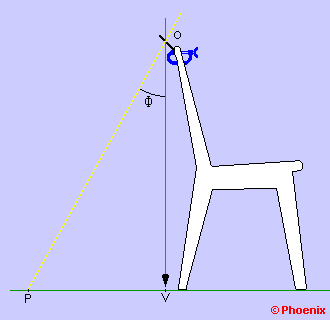
A preparação do local da medição deve ser feita com
antecedência.
A primeira parte (fase 1)
consiste em definir a linha norte-sul verdadeira;
vamos a ela:
fase 1
- Um ou dois dias antes do dia da medição, por volta das oito horas da
manhã coloque a cadeira numa área plana, lisa e ensolarada com a frente da
cadeira voltada para o norte. Se a cadeira for leve, coloque algo pesado sobre
o assento para evitar que ela se mova.
- Passe o fio do prumo pelo furo, determine e marque o ponto V sob a
vertical do furo. Use lápis ou caneta. Um traço de giz é muito grosso e
pode comprometer a precisão das medidas. Se for necessário, cole um pedaço
de papel no piso para facilitar o traçado.
- Usando um pedaço de barbante, ou uma régua com dois pregos como compasso,
trace um arco em torno deste ponto V com um raio aproximadamente igual
à altura do furo até o piso.
- O furo central deve projetar uma imagem do Sol, no piso, com aproximadamente
1 centímetro de diâmetro.
- Quando o centro da imagem do Sol cruzar o arco, marque o ponto M.
- A cadeira não pode ser movida! Por volta do meio dia, verifique onde está
a projeção do Sol. Esta área será a utilizada no dia da medição.
- Aguarde, na parte da tarde, que o Sol cruze novamente o arco e marque o
ponto T.
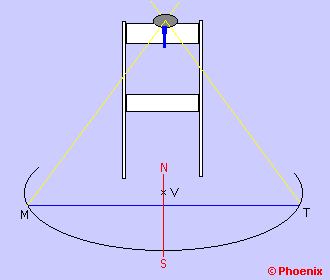
Usando o compasso, improvisado para fazer o arco, ache a
perpendicular à linha MT. Esta perpendicular à MT é a linha
norte-sul verdadeira. Esta linha pode ser traçada no piso ou marcada
por um fio esticado e as pontas fixadas com fita adesiva no piso. Se possível
deixe a cadeira no lugar até o dia da medição.
fase 2
- Verifique qual é o seu fuso horário. O leste do Brasil usa o fuso -
3. Os estados de Roraima, Pará, o centro-leste do Amazonas, Rondônia,
Mato Grosso e Mato Grosso do Sul usam o fuso - 4 e o Acre e o oeste do
Amazonas o de - 5 horas. Em seguida acerte o relógio a partir de uma 'estação
de rádio' que transmita sinais de tempo ou pelo telefone. Alguns canais de
televisão também transmitem sinais horários (de segundo em segundo)
enquanto estão se preparando para entrar no ar. O ideal é usar um relógio
grande, ou de cabeceira, para que várias pessoas possam anotar o momento do
trânsito ao sinal do observador.
fase 3
- Usando os mapas, e as coordenadas impressas em sua borda, encontre a sua
posição estimada em graus, minutos e segundos de
arco. Alguns mapas com escalas menores fornecem dados mais precisos, mas um
mapa de seu estado é suficiente. Este trabalho preliminar se destina a familiarizar o pesquizador com o sistema de coordenadas e permitirá conhecer o sentido de crescimento das coordenadas e as divisões do mapa. Faça interpolações e redivida a escala original se necessário.
A medição
No dia escolhido para a medição,
verifique a posição do anteparo usando o prumo, ou re-posicione se a cadeira
tiver sido movida. O ponto V deve estar exatamente sob o prumo do
anteparo.
Por volta do meio-dia, quando o centro da imagem do Sol cruzar a linha NS (Trânsito do Sol) marcamos o ponto P e registramos a hora com
precisão de segundos (h:min:seg). O erro de um segundo equivale a uma diferença de cerca de 400 metros na localização.
Em seguida meça com exatidão a altura OV
e a distância PA e anote os valores. A precisão das coordenadas vai
depender diretamente da precisão destas medidas.
Trabalhando com
frações de arco e de tempo
Para fazer contas com horas e ângulos
é necessário que os dados sejam compatíveis com o sistema decimal (base
10), mas eles são sempre fornecidos em horas, minutos e segundos ou graus,
minutos de arco e segundos de arco, no sistema sexagesimal (base 60).
Precisaremos então aprender a transformar uns nos outros.
1- Para transformar h:min:seg em horas
decimais, divida o número de minutos por 60 e o número de segundos por
3600. Em seguida some as parcelas.
Por exemplo, para 16h 18min 40s, fazemos: 18/60= 0,3 ; 40/3600= 0,0111 ;
16+03+0,0111 = 16,3111 horas decimais.
O mesmo procedimento é adotado para os ângulos.
2- Para fazer o inverso dessa transformação, ou seja, para
transformar horas decimais em h:min:seg,
separe a parte fracionária e multiplique por 60. Anote o número inteiro de
minutos. Separe novamente a parte fracionária e multiplique por 60. Anote o
número de segundos e suas frações.
Usando o resultado do exemplo anterior, 16,3111
horas decimais, fazemos: 0,3111 x 60 = 18,666 [separe esse 18]; 0,666 x
60 = 39,96. Assim teremos, 16 h 18 min 39,96 seg, ou seja, 16 horas, 18
minutos , 39 segundos e 96 centésimos do segundo. Quatro centésimos de
segundo foram perdidos nos arredondamentos, mas podemos desprezá-los. O
procedimento é similar para conversão de ângulos.
Cálculo da
posição
A partir dos valores OV e PV
nós poderemos calcular o ângulo F. A divisão OV/PV
fornecerá o valor da tangente trigonométrica do ângulo. Use a calculadora
para obter o arco tangente de OV/OP e você encontrará o ângulo F.
Se a medição foi feita nos dias de equinócios (20-março ou 22-setembro),
este ângulo é igual ao da latitude local. Se feita nos dias de solstícios
(21-junho ou 22-dezembro), ele deve ser corrigido de 23,45 graus (somar se for
solstício de verão, subtrair se solstício de inverno). Para outras datas,
usar os dados da declinação do Sol publicados nas tabelas do Anuário de
astronomia do Observatório Nacional. Transforme os valores decimais para
graus, minutos e segundos de arco. Compare o valor encontrado com a sua latitude
estimada. Se houver divergência sensível, refaça os cálculos.
Exemplo:
Suponhamos que você meça as distâncias no dia do equinócio (20 março) de OV= 787 milímetros (78,7 cm) e PV= 141 milímetros (14,1 cm).
- fazendo a conta PV/OV= 0,1792 ; este é o valor da tangente do ângulo que procuramos.
- usando a calculadora achamos o arco cuja tangente é 0,1792
- arc tg 0,1792 e encontramos 10,1574 (algumas calculadoras usam TAN-1 para arco tangente)
- para achar os minutos ( ' ) multiplicamos a parte fracionária por 60: 0,1574 x 60 = 9,4455
- para achar os segundos ( " ) multiplicamos a parte fracionária por 60: 0,4455 x 60 = 26,73 (vinte e seis segundos e setenta e três centésimos)
Podemos arredondar os 73 centésimos e usar 27 segundos.
Nossa latitude será então de 10º 9' 27" Sul.
Para o cálculo da longitude usaremos o Tempo Universal
(TU), ou Tempo Médio de Greenwich. Transforme todos os valores para o sistema
decimal. Para encontrar o TU do momento do trânsito, basta somar o número de
horas do fuso local ao valor registrado na medição.
Em seguida subtraia deste valor o do momento do trânsito em Greenwich no dia
correspondente.
Momento do
trânsito do Sol em Greenwich
| Data |
h:min:seg |
hora decimal |
| 20-mar-2005 |
12:07:27 |
12,1242 |
| 21-jun-2005 |
12:01:47 |
12,0297 |
| 22-set-2005 |
11:52:39 |
11,8775 |
| 22-dez-2005 |
11:58:39 |
11,9775 |
Multiplique o resultado por 15 (15º por fuso). O valor
encontrado é o ângulo em longitude. Converta este valor para graus, minutos
e segundos de arco. Compare o valor com a longitude de sua posição
estimada. Se houver diferença sensível, confira os cálculos.
Exemplo:
Suponhamos que o seu fuso horário é o de -4 horas e que a passagem meridiana do Sol foi às 12h 5min 15seg.
- transformamos este valor em horas decimais:
12 + 5/60 + 15/3600 = 12 + 0,0833 + 0,0041 = 12,0874
- somamos as horas do fuso local: 12,0874 + 4 = 16,0874
- subtraimos o momento da passagem meridiana em Greenwich: 16,0874 - 12,1242 = 3,9632
- multiplicamos o resultado por 15 para encontrar o ângulo decimal: 3,9632 x 15 = 59,448
- transformamos o ângulo decimal em graus, minutos e segundos de arco:
- separamos a parte fracionária e multiplicamos por 60: 0,448 x 60 = 26,88
- repetimos o procedimento para os segundos: 0,88 x 60 = 52,8
Assim teremos a longitude de 59º 26' 52,8" Oeste
As coordenadas do nosso exemplo serão então Lat. 10º 9' 27" Sul - Lon. 59º 26' 53" Oeste . Se procurarmos no mapa veremos que esta posição é próxima de Aripuanã, no estado de Mato Grosso.
Glossário
coordenadas
terrestres - latitude e longitude de um lugar no Sistema de Coordenadas
Geográficas (às vezes pode ser acrescentada a altitude)
equador - círculo imaginário que divide a
Terra em duas metades iguais, sobre o plano perpendicular ao eixo de
rotação.
equador celeste - projeção do equador sobre a
esfera celeste
equinócio - instante (ou ponto aparente) que o
Sol cruza o plano do equador
fuso horário - fatia em forma de fuso de 15
graus de largura entre dois meridianos
grau - 1/360 da divisão da circunferência.
GMT - Greenwich Mean Time = Tempo médio de
Greenwich
Greenwich - observatório próximo a
Londres-Inglaterra onde, por definição, passa o meridiano zero
latitude - ângulo medido entre o equador e um
ponto determinado da superfície terrestre em graus, minutos e segundos de
arco
longitude - ângulo medido entre dois planos
meridianos a partir do eixo terrestre em graus, minutos e segundos de arco
meridiano - arco imaginário sobre a
superfície da Terra no sentido norte-sul que liga os dois pólos
milha marítima - 1 minuto de arco sobre a
Terra (1.853 metros)
milha terrestre - 1.000 passos (pé direito) de
uma centúria (1.440 metros)
minuto de arco - 1/60 do grau (equivale a 1.853 metros sobre a Terra)
nó - velocidade equivalente a uma milha
marítima por hora
paralelo - círculo imaginário sobre a
superfície da Terra, perpendicular a seu eixo. O círculo máximo é chamado
equador
passagem meridiana - instante que um astro
cruza o meridiano de um lugar
plano meridiano - plano que contém o eixo da Terra e um ponto sobre sua superfície
posição geográfica - coordenadas de um lugar
segundo de arco - 1/60 do minuto de arco ou
seja, 1/3.600 do grau (equivale a 30,8 metros sobre a Terra)
solstício - instante (ou ponto aparente) em
que o Sol atinge a máxima latitude (23,45 graus) norte ou sul
TL - ou LT - Tempo
Legal, tempo oficial de cada fuso horário
trópico - paralelo sobre o qual o Sol atinge o
solstício
TU - ou UT - Tempo
Universal = GMT




