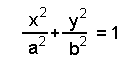
- Como é a equação para cálculo da posição de um planeta?
- O cálculo da
posição de um planeta foi a maior obra de Johannes Kepler, que
primeiro conseguiu equacionar suas órbitas, usando os dados
coletados por seu mestre, Tycho Brahe. Estes cálculos se baseiam
nas três leis, hoje conhecidas como leis de Kepler:
1- As órbitas
de um planeta são elipses e o Sol ocupa um de seus fócos.
2- A velocidade orbital é tal que o raio
vetor varre áreas iguais em tempos iguais.
3- O quadrado do período de revolução é proporcional ao cubo da distância média ao Sol.
Alguns livros
de astronomia costumam trazer gráficos para a localização dos
planetas, mas não conseguem precisar sua posição.
A equação
para as órbitas planetárias, é a equação geral das elipses:
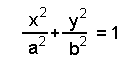
Onde x e y fornecem a posição do planeta no plano de coordenadas. a e b
são respectivamente os semi-eixos maior e menor da elipse.
O problema é posicionar esta elipse no espaço. Para isso você terá de ter
em mãos os sete elementos orbitais que equacionarão a órbita:
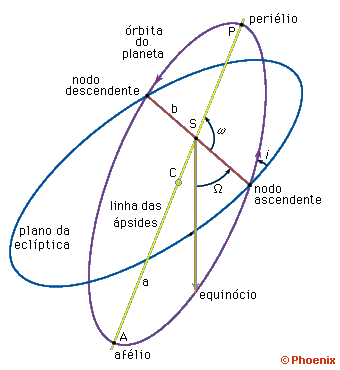
onde:
a= semi eixo maior da elipse
e= excentricidade da órbita
i= inclinação da órbita em relação ao plano da eclíptica
W= longitude do nodo ascendente
w= argumento do periélio
T= instante da passagem pelo periélio
n= o movimento médio
Estes parâmetros, aliados ao tempo decorrido desde a passagem pelo periélio, fornecerão a posição do planeta, mas quando verificamos a sua posição real, observamos que ainda existem muitas correções a serem feitas devido à perturbação gravitacional dos outros planetas, que afetam reciprocamente suas órbitas de maneira muito complexa. Centenas de parâmetros têm de ser computados. Para calcular esta interação, hoje são usados computadores rápidos que geram tabelas com precisão bastante alta, mas que ainda contêm erros na ordem de alguns minutos. Como você pode ver, não existe uma equação única para a solução do problema, e sim uma série de procedimentos.
Um resumo deste trabalho seria mais ou menos assim:
Você aplica
na fórmula da elipse o semi-eixo maior e a excentricidade para
determinar a equação que atende à sua órbita.
Em seguida você tem que calcular a anomalia excêntrica e a
anomalia verdadeira através da fórmula da área da elipse.
Usando a fórmula de Kepler você calculará a anomalia média e
o movimento médio. Com o movimento médio você calcula o
período e a constante de proporcionalidade, e a velocidade
areolar.
Para posicionar o planeta sobre esta órbita você terá que
calcular o tempo decorrido Dt entre
o T,
que é o instante da passagem do
planeta pelo periélio e a data desejada. Este dado é fornecido
como dia juliano, calculado a partir do momento desejado
(ano, mês, dia, hora e fração). Baseado na diferença de tempo
decorrido você pode plotar o planeta sobre a curva.
Pronto! O problema está resolvido no plano. Mas o planeta e sua órbita estão no espaço: teremos de usar coordenadas espaciais.
Assim sendo, a equação obtida será posicionada sobre um
referencial com a origem no Sol (sistema heliocêntrico) usando a geometria esférica. Para isso você usará a inclinação da órbita, a
longitude do nodo ascendente e o argumento do periélio.
Depois que estas equações estiverem prontas, teremos de trazer a
origem para o nosso ponto de vista, ou seja, para a posição da
Terra, passando do sistema heliocêntrico para o sistema
geocêntrico. Esta mudança exige que a Terra já esteja
localizada no espaço, num sistema de equações similar ao do
trabalho.
Após reduzidas à posição topocêntrica, local do
observador, os raios vetores e seus ângulos são transformados
em Ascensão Reta e Declinação, que são os dados da posição
do astro.
Esta é a parte simples do problema, que não leva em
consideração as perturbações gravitacionais dos outros
planetas. Para isso, são incluídas equações diferenciais para
cada um dos planetas envolvidos.
As equações diferenciais são solucionadas pelo sistema de
aproximações sucessivas, isto é, calcula-se um valor base que
é realimentado e gera um novo valor, que é novamente
realimentado, até que se consiga a precisão necessária. É por
isso que são usados computadores de alta velocidade!
Um dos maiores triunfos da mecânica celeste usando estas
técnicas foi a descoberta do planeta Netuno em 1846 a partir das
perturbações causadas pelo movimento de Urano, numa época que os cálculos eram feitos a lápis.
Como vimos, não existe uma fórmula para o cálculo da posição do planeta e sim uma série complexa de procedimentos.
Estes dados são tabelados e publicados regularmente nos anuários do Observatório Nacional.