Os cálculos estão no final deste texto, até a oitava casa decimal e distinguindo os dois níveis de maré alta. Realmente, a segunda maré alta será um pouco menor do que aquela voltada diretamente para a Lua.
É conveniente introduzir este assunto com algumas explicações adicionais que facilitem a compreensão do tópico aos alunos de ensino médio do Professor Igor.
Faço uma observação adicional para evitar alguma má interpretação:
considero para efeitos desta explicação a utilização da denominação 'força centrifuga' como a força que aponta para fora de um sistema em rotação (origem inercial).
Uso também esta expressão para expressar a inércia atuante sobre um corpo fluido 'solto'.
Possivelmente tenha cometido alguns erros e simplificações, mas alguém as poderá corrigir e usar este texto para melhorar a discussão desse assunto.
Espero não estar tão errado. Se estiver, façam as correçoes necessárias nos conceitos utilizados e nos calculos efetuados que eu também vou aprender algo a mais, como aprendi que existia uma segunda maré alta ... :>) (praia pra mim significa verão e é para aproveitar e descansar, entende ... :>) (sou morador de cidade não litoranea)
A condição necessária e suficiente para criar duas marés altas e duas marés baixas é dada pela seguinte observação:
Nos locais onde há maré alta, a resultante das forças gravitacionais e centrifugas que atuam nestes pontos deve ser menor que a resultante das forças gravitacionais que atuam nos locais onde há maré baixa.
Nestes pontos de maré alta, a intensidade resultante do somatório de forças que atuam sobre estes pontos deve decrescer em relação aos medidos nos pontos de maré baixa. Uma diminuição desta força resultante forçará as massas líquidas a se deslocarem para uma nova acomodação estável destas massas (por inércia-> para uma nova órbita, conforme o Zeca já tinha mencionado).
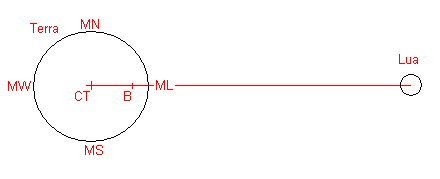
A análise a seguir leva em conta as seguintes definições:
4 pontos MN,MS,ML e MW para os quais serão calculadas a variação de
intensidade de campos gravitacionais e acelerações centrifugas.
Por uma questão de simplificação M é Maré e N,S,L,W Norte, Sul, Leste,
Oeste).
CT-Lua define o eixo entre os centros da Terra e da Lua.
ML é a maré alta provocada na Terra pelo lado exposto à Lua.
MW é a maré alta no lado oposto da Terra em relação à ML.
B baricentro do sistema Terra-Lua

Quais são as principais forças atuantes nestes pontos?
campo gravitacional da Terra
campo gravitacional da Lua
aceleração centrifuga do Sistema Terra-Lua
aceleração centrifuga da Terra
Desconsidero a influência do Sol, que também cria algumas mudanças nos valores calculados, mas ... os calculos mostram que a variação de força que realmente está causando o efeito de 2 marés é devido `a força centrífuga criada pela rotação do sistema Terra-Lua combinada com a atração do campo gravitacional da Lua
Dados Utilizados:
Constante gravitacional (G) = 6,67 E-11 m3kg-1s-2
diametro da Terra = 12.756 km
distancia Terra a Lua = 384.000 km
distancia Terra a Lua lado direto = 377.622 km
distancia Terra a Lua lado oposto = 390.378 km
Massa da Lua = 7,4 E22 kg
T=Periodo de rotação do Sistema Terra-Lua = 27,3 dias = 2.358.720 seg
Raio da Terra = 6.378 km
Posição do baricentro do sistema Terra-Lua= a 4.671 km do centro da
Terra ou a 1.707 km da superficie exposta voltada à Lua (maré alta)
Posição da superficie terrestre em oposição à Lua (em relação ao
baricentro)= 11.009km (ponto da segunda maré alta)
Fórmulas:
ac= v2/R
g= G.M1/R2
v=d/t
Forças normais à superficie nestes pontos:
Considera-se positiva (+) a força que aponta para o centro do planeta Terra.
Negativo (-) a força que aponta para fora do planeta.
Forças tangenciais à superficie nestes pontos: (~) Não afetam elevação ou diminuição de nível das partes fluidas, podendo provocar um movimento apenas lateral, paralelo ao nível do mar.
Os calculos apresentam a contribuição das acelerações nos 4 locais :
Siglas:
gT= gravidade na Terra
gL=gravidade da Lua
acB= aceleração centrifuga criada pela rotação do Baricentro do sistema
Terra-Lua
acT= aceleração centríguga criada pela rotação da Terra
aR= aceleração resultante
#9,8 = diferença entre a aceleração do campo gravitacional terrestre e seu
valor
nominal em 9,80000000. O valor exato de g não é significativo pois este é
290 vezes
maior que a maior contribuição dada por qualquer outra aceleração
Maré Alta= aceleração resultante útil para criar o efeitos de 2 marés altas
Obs. Não foi incluida para efeito de cálculos a declinação do eixo
terrestre.
| MBN | MBS | MAW | MAL | |
| gT | +9,80000000 | +9,80000000 | +9,80000000 | +9,80000000 |
| gL | ~(0,00003347) | ~(0,00003347) | +0,00003239 | -0,00003461 |
| acB | ~(0,00003311) | ~(0,00003311) | -0,00007804 | -0,00001210 |
| acT | -0,03373003 | -0,03373003 | -0,03373003 | -0,03373003 |
| aR | +9,80000000 | +9,80000000 | +9,76622432 | +9,76622326 |
| #9,8 | +0,00000000 | +0,00000000 | -0,03377568 | -0,03377674 |
| Maré Alta | +0,00 | +0,00 | -0,00004565 | -0,00004671 |
Os cálculos devem levar em consideração que os corpos Terra e Lua formam um sistema de massa com baricentro bem definido. Talvez esta seja a parte mais difícil de entender e geralmente esquecida Vamos a uma tentativa de explicação:
O que realmente orbita o Sol, com uma velocidade aproximadamente constante
é o baricentro do Sistema Terra-Lua. Se nosso ponto de observação for
deslocado
para as proximidades do Sol, veremos a Lua girando ao redor da Terra, numa
espécie de bamboleio.
Num determinado instante vê-se a Terra e a Lua em
quadratura (com a Lua a direita). Após metade do periodo de rotação do
sistema
Terra-Lua (27,3 dias / 2 = 13,65 dias) Terra e Lua estão novamente em
quadratura.
só que a Lua agora estará a esquerda da Terra.
Um telescópio apontado para
a Terra e este estando no centro da ocular e com um perfeito sistema de
acompanhamento
que permita 13,65 dias depois apontar novamente o telescópio para a Terra
não
mostrará mais a Terra ocupando o centro da ocular, pois o que realmente
estaria sendo
acompanhado pelo perfeito sistema de acompanhamento seria seu baricentro,
que é
quem realmente está em revolução ao redor do Sol.
É claro que um perfeito sistema de acompanhamento faria as correções necessárias para corrigir e reapontar novamente para que na ocular se visse novamente a Terra ao centro. Este movimento é real e cria realmente uma força centrifuga como em qualquer outro sistema de corpos que gire em torno de algo ou de si mesmo e dessa forma deve ser incluido para cálculo da resultante das forças nos pontos que definem as marés.
Acho que é isso.
Henry Jung