 |  |
As superfícies refletoras dos telescópios são superfícies geradas pela rotação de curvas cônicas, também conhecidas como curvas naturais. Elas são as elipses, as parábolas e as hipérboles. Estas curvas são definidas como a intersecção de um cone por um plano que não passe pelo seu vértice. Se girarmos 180 graus um plano que passe por uma reta ortogonal ao eixo do cone poderemos simular toda esta família de curvas.
Para vizualizar estas curvas no espaço vamos simular a intersecção de um cone por um plano, inicialmente vertical que gira 180 graus em torno de uma reta horizontal no sentido horário.
| |
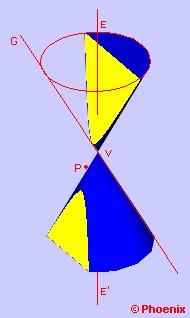
Imagine um cone definido por uma reta geratriz G que gira em torno de um eixo E que passa pelo ponto V. O ponto V será o vértice de dois cones opostos de tamanho ilimitado. Imagine que, por um ponto P genérico, externo ao cone e abaixo do ponto V, passa uma reta, perpendicular ao plano da tela.
Suponhamos que por este ponto passe um plano vertical, representado pela linha azul, que contem esta reta.
Nesta situação o plano corta ambas as folhas do cone, e esta intersecção cria uma hipérbole de dois ramos. Vamos agora girar este plano em torno do ponto P, no sentido horário.
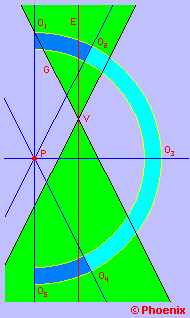
Enquanto este plano se encontra entre a posição vertical, paralela ao eixo E, e antes de chegar à paralela à geratriz do lado oposto, sua intersecção com o cone gera uma família de hipérboles 
.
Quando a inclinação deste plano for igual à da geratriz do cone, no ponto O2, só teremos uma intersecção no cone, e ela terá a forma de uma parábola 
.
A parábola pode ser considerada como um caso especial das hipérboles ou das elipses, onde um dos focos está a uma distância infinita.
Quando o plano ultrapassa ligeiramente este ponto, a curva se fecha sobre uma única folha do cone e forma uma elipse muito excêntrica. À medida que giramos o plano a excentricidade vai diminuindo até o ponto O3 em que o plano fica perpenducular ao eixo E, mas a partir daí começa a crescer novamente 
.
No ponto O3 quando o nosso plano fica exatamente perpendicular ao eixo E a intersecção formará uma curva notável: uma elipse de excentricidade zero - a circunferência.
Quando atingimos o ponto O4, de novo estaremos com nosso plano paralelo à geratriz e uma parábola, desta vez invertida, será formada pela intersecção do plano com o cone. Avançando mais um pouco retornamos ao domínio das hipérboles até que o plano esteja novamente vertical ao chegar ao ponto O5.
Se tormarmos o plano que seccionou o cone como referência, temos como equacionar a curva e estudá-la de forma mais simples 
.
A hipérbole é o lugar geométrico dos pontos de um plano cujas distâncias a dois pontos fixos (focos) desse plano têm diferença constante.
Isto significa que a diferença entre os segmentos AF e AF' é constante; a curva se desenvolve a partir do eixo que une os dois focos e segue assintoticamente (tendem a se encontrar no infinito) a duas retas que se cruzam no centro. O ângulo entre as retas concorrentes define a abertura da hipérbole.
A parábola é a curva mais popular das cônicas e é conhecida de todos os estudantes de física, por ser muito usada no estudo dos fenômenos de queda dos corpos. 
.
A parábola é o lugar geométrico dos pontos de um plano eqüidistantes de um ponto fixo (foco) e de uma reta fixa (diretriz).
A distância AF é igual à distancia AB, sendo que B está sempre sobre a diretriz. A parábola é a curva que dá origem aos espelhos parabolóides, muito usados nas antenas de TV e dos rádiotelescópios, e é claro, na maioria dos telescópios ópticos.
A elipse é conhecida do todo astrônomo. É a base de quase todas as órbitas de corpos celestes 
e o corpo mais massivo ocupa sempre um dos focos.
A elipse é o lugar geométrico dos pontos de um plano cujas distâncias a dois pontos fixos (focos) desse plano têm soma constante.
Assim a soma dos segmentos AF e AF' é constante. A elipse pode gerar superfícies de revolução diferentes quando girada em torno do eixo maior, o elipsóide de revolução, ou em torno do eixo menor, que chamamos de elipsóides oblatos (achatados nos polos).
Chamamos anesférica ou asférica a uma superfície que tem raio de curvatura variável, em contraposição a uma superfície esférica que tem um raio constante.
À variação do raio medida sobre o eixo óptico chamamos de "aberração longitudinal" que representamos por Dp'.
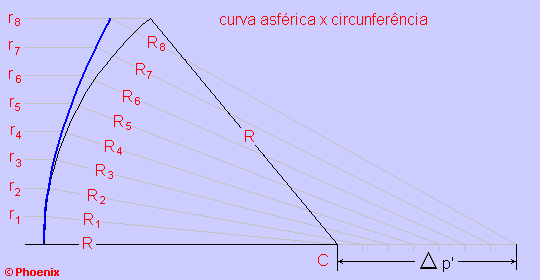
Como vemos na figura, para cada raio da objetiva r teremos um raio de curvatura R acrescido de um Dp'. Quando estamos calculando a aberração longitudinal de espelhos côncavos, usamos a fórmula simplificada:
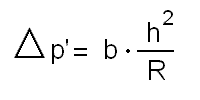
Nesta fórmula o coeficiente b nos dará a deformação da curva indicada 
pelo arranjo do nosso projeto.
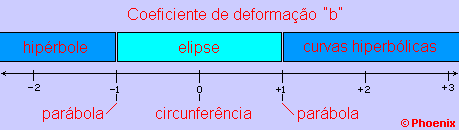
No caso dos espelhos esféricos o valor de b = 0 nos indica que não existe aberração longitudinal para uma imagem colocada no centro de curvatura.
Para espelhos elípticos o valor de b pode estar entre -1 < b < +1, sendo que os valores entre -1 e 0 formam elipsóides gerados pela rotação da elipse em torno do eixo maior e valores entre 0 e +1 formam elipsóides oblatos (achatados nos pólos) gerados pela rotação em torno do eixo menor da elipse. Os espelhos ainda podem ser sub ou sobre-corrigidos 
, dependendo do acrescimo ou da dedução da aberração longitudinal. Os sinais + ou - nos indicam o sentido do Dp'.
Valores menores que -1 gerarão sempre hiperbolóides, tanto mais deformados quanto maiores forem os módulos destes valores.
Valores maiores que +1 gerarão curvas hiperbólicas de formas variadas. O inverso de uma delas gera o perfil da lâmina corretora dos telescópios Schmidt (y=senh[x]).
